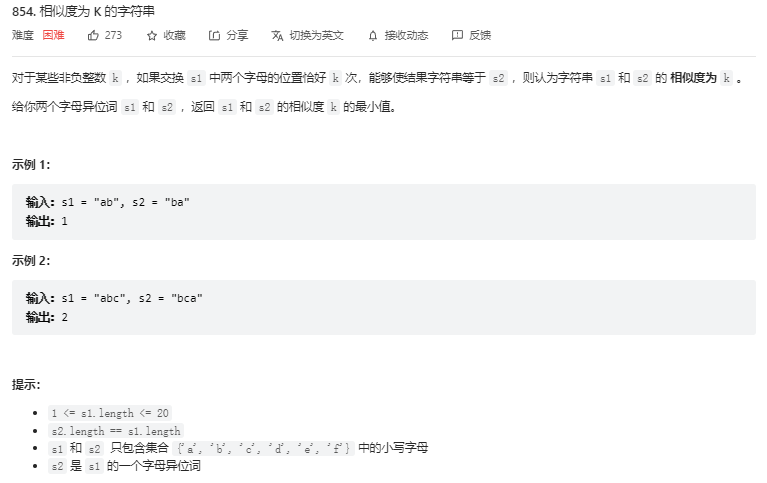
题目分析
本题根据数据范围,可以推测是一个爆搜的题目,但是数据范围又超过了爆搜上限,因此需要考虑如何剪枝。
广度优先搜索
本题的思路是,可以找到第一个不相等的索引,然后与后面每一位不相等的交换。如果出现了结果,则直接return即可。
BFS的模板大家都很熟了,直接看代码即可。因为两个词是异位词,所以不会交换20次,估计也就是10次左右,因此爆搜也是可以通过的。
本题最好是加上一个哈希表,记录已经搜索过的字符串。
算法的**时间复杂度为O(6^n),空间复杂度为O(6^n)**。因为本题的特殊性和剪枝,所以会远远小于这个值。
1 | class Solution { |
深度优先搜索
能通过BFS算法求解的大部分也都可以使用DFS,重要的是剪枝函数如何取写。
除了常规的记忆化:当搜到某个字符串,并且需要的交换次数大于记录的值,则直接返回即可。
更巧妙的是引入一个minSwap的函数,表示当前字符串str与s2最少的交换次数,最少的交换次数是两个字符的差异(diff + 1) / 2,因为是都当作两两交换可以求得的最少交换次数。
如果当前的步骤step + 两个字符串的最少交换次数都大于res,则也不需要遍历了。
算法的**时间复杂度为O(6^n),空间复杂度为O(6^n)**。因为本题的特殊性和剪枝,所以会远远小于这个值。
1 | class Solution { |
A star
A star算法是一种常见的寻路算法,其本质是一个贪心的BFS。
我们可以想一下,如果BFS的第一步可以得到两个结果,一个距离结果更远,一个距离结果更近,我们是否需要按照顺序先遍历距离结果更远的那条路?
我们假设从起点到某个字符串str1,需要交换a次,str1与答案s2距离为b。从起点到另一个字符串str2,需要交换c次,str2与答案距离为d。
如果a + b > c + d,是否可以先搜索str2,这就是A star算法的核心思想。
实现也很简单,只需要维护一个最小堆,将堆顶元素取出遍历即可。
算法的**时间复杂度为O(6^n),空间复杂度为O(6^n)**。因为本题的特殊性和剪枝,所以会远远小于这个值。
1 | class Solution { |
刷题总结
本题的三种方法希望小伙伴们都可以熟练掌握。一定要独立完成本题呀。